Расчеты показывают [3.5], что возмущенная орбита НС в общем случае не будет эллиптической, и истинные параметры орбитального движения НС отличаются от параметров, рассчитанных по формулам не возмущенного (кеплерова) движения.

При анализе возмущенного движения НС принято считать, что НС в ка­ждый момент времени находится на той невозмущенной (эллиптической) ор­бите, которая рассчитана с учетом прекращения в этот момент действия воз­мущающих сил. Это означает, что в отличие от невозмушенного движения элементы возмущенной орбиты НС непостоянны. Их изменение происходит непрерывно, но каждому моменту времени и каждой точке возмущенной тра­ектории соответствует своя кеплерова орбита, которую называют оскулирующей, а ее орбитальные элементы - оскулирующими. Для расчета возмущенных пространственных координат НС и их произ­водных аппаратура потребителя получает от НС периодически обновляемые оскулируюшие элементы и поправки к ним. Расчет в приемоиндикаторе проводится с целью уточнения параметров движения НС на момент времени ti по данным эфемерид, которые содержатся в разделе оперативной информации навигационного сообщения, даются на моменты времени tb и обновляются через каждые 15 мин, поэтому для вре­мени ti определяется как | tb - t i| £ 15 мин.Процедура пересчета проводится численным интегрированием диффе­ренциальных уравнений орбитального движения НС. Начальными условия­ми для интегрирования системы уравнений являются данные эфемерид. Уравнения возмущенного движения НС, используемые при расчетах в СРНС ГЛОНАСС, кроме цен­тральной силы притяжения Земли учитывают дополнительную силу, обуслов­ленную полярным сжатием и характеризуемую гармоникой С20 , а также лун­но-солнечные гравитационные возмущения:

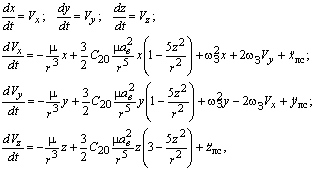
тут ае - экваториальный радиус Земли,

При интегрировании уравнений лунно-солнечные гравитационные ускорения () полагаются постоянными величинами на интервалах ±15 мин.

Ин­тегрирование проводится классическим одношаговым методом Рунге-Кутта четвертого порядка.

Пересчет координат потребителя из земной в геодезическую систему координат

Алгоритм оценки навигационных параметров (1.83) формирует оценки вектора потребителя в геоцентрической системе координат OXYZ, связанной с Землей. Потребителя во многих случаях интересуют свои координаты в геоде­зической системе координат. Поэтому в ПИ необходимо осуществить пересчет координат из геоцентрической системы (координаты х, у, z ) в геодезическую (координаты B - геодезическая широта, L- геодезическая долгота, H- геодезическая высота). О6щие формулы связи двух систем координат имеют следующий вид:

,

где ;

- эксцентриситет эллипсоида;

- параметр сжатия эллипсоида.

Пересчет по этим выражениям может быть реализован следующим вычислительным алго­ритмом [12.5]:

1) исходные данные координаты х, у, z в геоцентрической системе координат OXYZ; выходные данные - координаты B, L, H в геодезической системе координат:

2) вычисляется вспомогательная величина

;

3) анализируется значение D:

если D = 0 , то В = z / (2|z|) ; L = 0 ; Н = z sin В - ;

если D > 0, то La = arcsin(y / D);

при этом если х > 0, у > 0, то L = La

4) анализируется значение z:

если z = 0, то В = 0, H = D - а;

в других случаях находятся вспомогательные величины r, с, р

реализуется итеративный процесс