Разработка алгоритмов контроля и диагностики системы управления ориентацией космического аппаратаСтраница 20
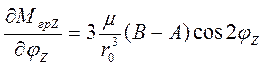 ;
;
при ![]() и при
и при ![]() имеет разные знаки. Какое из этих двух положений соответствует статистической устойчивости, зависит от знака (B-A) [1, 3, 8]. Условие устойчивости (возникновение восстанавливающего момента при малом отклонении)
имеет разные знаки. Какое из этих двух положений соответствует статистической устойчивости, зависит от знака (B-A) [1, 3, 8]. Условие устойчивости (возникновение восстанавливающего момента при малом отклонении)  реализуется при
реализуется при ![]() для A>B или при
для A>B или при ![]() для B>A, т.е. в обоих случаях вытянутая ось тела должна занимать вертикальное положение.
для B>A, т.е. в обоих случаях вытянутая ось тела должна занимать вертикальное положение.
Таким образом, вытянутое в вертикальном положении тело, обладая статистической устойчивостью по тангажу и крену, является нейтральным по отношению к углу рыскания [1, 3, 4].
3.3 Гироскопический измеритель угловой скорости
Для пересчета векторов сил, моментов и т.д. из одной системы координат в другую необходимо вычислить матрицу перехода, элементами которой являются косинусы углов между осями исходной и повернутой систем координат [1, 3, 21]. Эта матрица определяется последовательностью углов поворота, которые позволяют перейти от одной системы координат к другой. Осуществление такого рода перехода требует не более трех поворотов исходной системы координат. Выбор последовательности углов поворота обычно определяется физическим содержанием задачи [1, 3, 5]. Это могут быть углы, измеренные с помощью приборов системы управления, от которых зависят аэродинамические и другие нагрузки на ЛА и т.д. [1]
Применение направляющих косинусов в космических приложениях обусловлено, прежде всего, тем, что они могут быть непосредственно измерены на борту космического аппарата [5].
1. Сформируем матрицу dA [3,3] – переход от ССК к ПСК ГИВУС:
| ССК | ||||
| ПСК | x | y | z | |
| x | d[1,1] | d[1,2] | d[1,3] | |
| y | d[2,1] | d[2,2] | d[2,3] | |
| z | d[3,1] | d[3,2] | d[3,3] | |
|
Матрица dА получается вследствие трех элементарных поворотов:
1) вокруг оси х на ÐАД(1):


Рис.3.7 - Схема поворота первого типа вокруг оси х
Матрица направляющих косинусов:
 ;
;
2) вокруг оси y на ÐАД(2):
|

